It is common to use circular queues in a data structure in operating systems. It is used to manage the execution of computing processes or programs. You use a circular queue as a buffer to store the processes in order of their insertion and then remove them at the time of resource allocation or execution. In this tutorial, you will explore a circular queue in a data structure along with its implementation and applications.
Why Was the Concept of Circular Queue Introduced?
Implementation of a linear queue brings the drawback of memory wastage. However, memory is a crucial resource that you should always protect by analyzing all the implications while designing algorithms or solutions. In the case of a linear queue, when the rear pointer reaches the MaxSize of a queue, there might be a possibility that after a certain number of dequeue() operations, it will create an empty space at the start of a queue.
Additionally, this newly created empty space can never be re-utilized as the rear pointer reaches the end of a queue. Hence, experts introduced the concept of the circular queue to overcome this limitation.
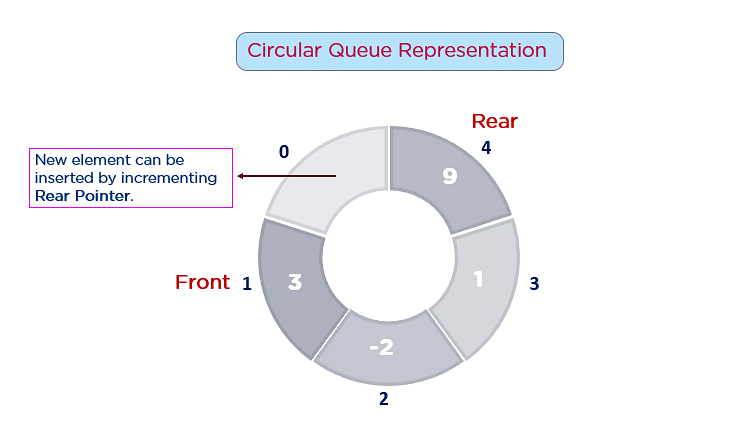
As shown in the figure above, the rear pointer arrives at the beginning of a queue with the help of a circular link to re-utilize the empty space to insert a new element. This simple addition of a circular link resolves the problem of memory wastage in the case of queue implementation. Thus, this particular type of queue is considered the best version of a queue data structure.
What is Circular Queue in a Data Structure?
A circular queue is an extended version of a linear queue as it follows the First In First Out principle with the exception that it connects the last node of a queue to its first by forming a circular link. Hence, it is also called a Ring Buffer.
As shown in the illustration above, the circular queue resolves the memory wastage problem with the help of a circular link.
How Does the Circular Queue Work?
The Circular Queue is similar to a Linear Queue in the sense that it follows the FIFO (First In First Out) principle but differs in the fact that the last position is connected to the first position, replicating a circle.
Operations
- Front - Used to get the starting element of the Circular Queue.
- Rear - Used to get the end element of the Circular Queue.
- enQueue(value) - Used to insert a new value in the Circular Queue. This operation takes place from the end of the Queue.
- deQueue() - Used to delete a value from the Circular Queue. This operation takes place from the front of the Queue.
Representation of Circular Queue using Arrays and a Linked List
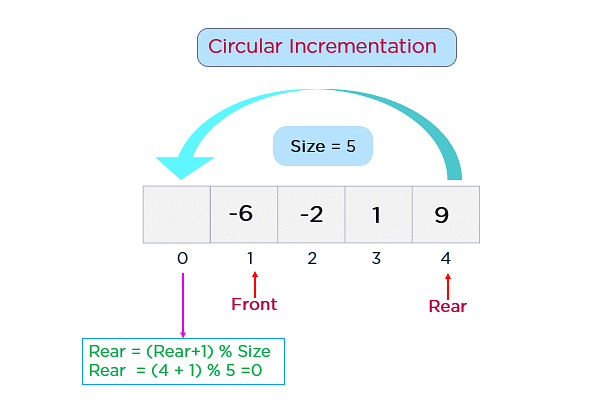
You can implement the circular queue using both the 1-D array and the Linked list. However, implementing a circular link is a new addition that you need to execute. Additionally, this queue works by the process of circular incrementation. That is, when you reach the end of a queue, you start from the beginning of a queue. The circular incrementation is achievable with the help of the modulo division.
Now you will understand how you can achieve circular incrementation, with the help of an example. Let’s say the MaxSize of your queue is 5, and the rear pointer has already reached the end of a queue. There is one empty space at the beginning of a queue, which means that the front pointer is pointing to location 1.
Rear + 1 = 4 + 1 = 5 (Overflow Error) Rear = (Rear + 1)% MaxSize = 0 (Reached loc. 0 / Beginning of queue) |
Similarly, the tail node of a linked list can be connected to its head node by adding the address value of a head node in the reference field of the tail node.
Steps for Implementing Queue Operations
Enqueue() and Dequeue() are the primary operations of the queue, which allow you to manipulate the data flow. These functions do not depend on the number of elements inside the queue or its size; that is why these operations take constant execution time, i.e., O(1) [time-complexity]. Here, you will deal with steps to implement queue operations:
1. Enqueue(x) Operation
You should follow the following steps to insert (enqueue) a data element into a circular queue -
- Step 1: Check if the queue is full (Rear + 1 % Maxsize = Front)
- Step 2: If the queue is full, there will be an Overflow error
- Step 3: Check if the queue is empty, and set both Front and Rear to 0
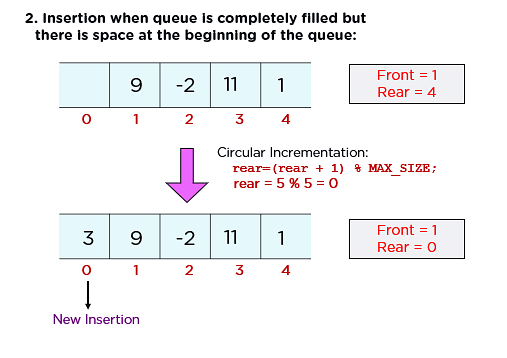
- Step 4: If Rear = Maxsize - 1 & Front != 0 (rear pointer is at the end of the queue and front is not at 0th index), then set Rear = 0
- Step 5: Otherwise, set Rear = (Rear + 1) % Maxsize
- Step 6: Insert the element into the queue (Queue[Rear] = x)
- Step 7: Exit
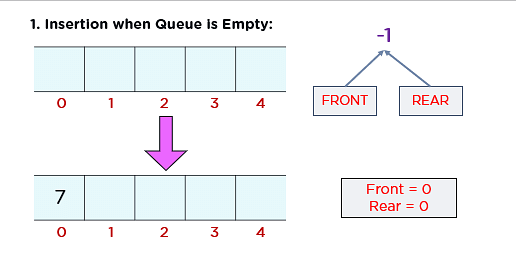
Now, you will explore the Enqueue() operation by analyzing different cases of insertion in the circular queue:
2. Dequeue() Operation
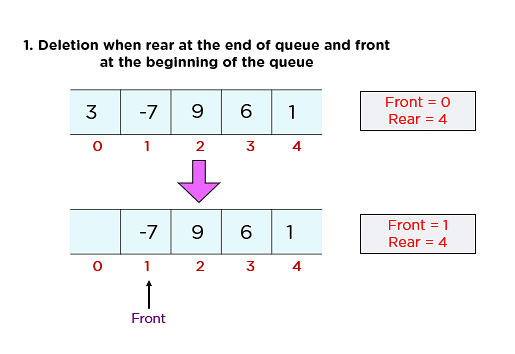
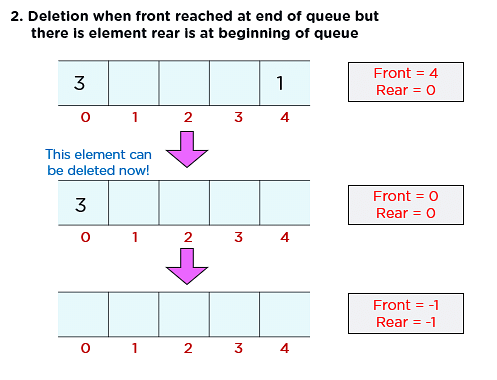
Obtaining data from the queue comprises two subtasks: access the data where the front is pointing and remove the data after access. You should take the following steps to remove data from a circular queue -
- Step 1: Check if the queue is empty (Front = -1 & Rear = -1)
- Step 2: If the queue is empty, Underflow error
- Step 3: Set Element = Queue[Front]
- Step 4: If there is only one element in a queue, set both Front and Rear to -1 (IF Front = Rear, set Front = Rear = -1)
- Step 5: And if Front = Maxsize -1 set Front = 0
- Step 6: Otherwise, set Front = Front + 1
- Step 7: Exit
Let’s understand Dequeue() operation through a diagrammatic representation:
Implementation of Circular Queue using an Array
The process of array implementation starts with the declaration of array and pointer variables. You use the following statements for it:
#define MAX_SIZE 5 //global value assignment to max_size variable int a[MAX_SIZE]; int front = -1; int rear = -1; |
After this, you will begin with the implementation of circular queue operations.
1. The first primary queue operation that allows you to manage data flow in a queue is Enqueue(). For implementing this function, you have to check if the queue is empty. If a circular queue is empty, you must set both the front and rear pointer to 0 manually. This condition can be implemented as follows:
void enqueue(int x) { if (front == -1 && rear == -1) { front = rear = 0; } |
Later, you will check if the queue is full. If it’s full, you will return an overflow error (i.e., no empty space for insertion).
else if ((rear + 1) % MAX_SIZE == front) { printf("queue is full\n"); return; } |
Otherwise, you must increment the rear pointer using the technique of circular incrementation. And as the rear pointer is incremented now, you can insert an element at the new location.
else rear = (rear + 1) % MAX_SIZE; a[rear] = x; } |
2. The next operation is Dequeue(). The Dequeue() operation removes the element from the front node of a queue. Further, an element can only be deleted when there is at least an element to delete, i.e., Rear > 0 (queue shouldn’t be empty). If the queue is empty, then you must write an underflow error and exit.
void dequeue() { if (front == -1 && rear == -1) { printf("queue is empty \n"); return; } |
Additionally, if there is only one element in the queue, you should set both the front and rear pointer to NULL.
else if (front == rear) { front = rear = -1; } |
Otherwise, you will simply increment the front pointer using the technique of circular incrementation. And as the front pointer is incremented, the link to the previous element’s memory address gets removed, resulting in the deletion of a previous element.
else front = (front + 1) % MAX_SIZE; } |
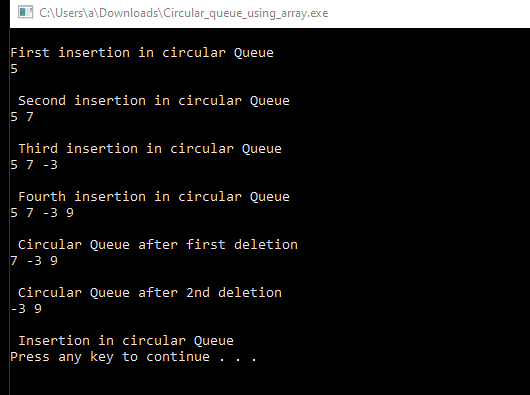
The complete program for the array implementation of a circular queue in programming language C is given below. The code consists of two additional functions Peek() and Print(). The Peek() function returns the element at the front node of a queue without deleting it. Meanwhile, the Print() function is created to visualize the state of a queue after each operation.
Program in C:
#include <stdio.h> #include <Windows.h> #define MAX_SIZE 5 int a[MAX_SIZE]; int front = -1; int rear = -1; void enqueue(int x) { if (front == -1 && rear == -1) { front = rear = 0; } else if ((rear + 1) % MAX_SIZE == front) { printf("queue is full\n"); return; } else rear = (rear + 1) % MAX_SIZE; a[rear] = x; } void dequeue() { if (front == -1 && rear == -1) { printf("queue is empty \n"); return; } else if (front == rear) { front = rear = -1; } else front = (front + 1) % MAX_SIZE; } int Peek() { if (a[front] == -1) return -1; return a[front]; } void Print() { int count = ((rear + MAX_SIZE - front) % MAX_SIZE)+1; int i; for (i = 0; i < count; i++) { printf("%d ", a[(front+i)%MAX_SIZE]); } printf("\n"); } int main(void) { enqueue(5); printf("\nFirst insertion in circular Queue\n"); Print(); printf("\n Second insertion in circular Queue\n"); enqueue(7); Print(); printf("\n Third insertion in circular Queue\n"); enqueue(-3); Print(); printf("\n Fourth insertion in circular Queue\n"); enqueue(9); Print(); printf("\n Circular Queue after first deletion\n"); dequeue(); Print(); printf("\n Circular Queue after 2nd deletion\n"); dequeue(); Print(); printf("\n Insertion in circular Queue\n"); enqueue(14); system("pause"); return 0; } |



కామెంట్లు లేవు:
కామెంట్ను పోస్ట్ చేయండి